Charles Meneveau

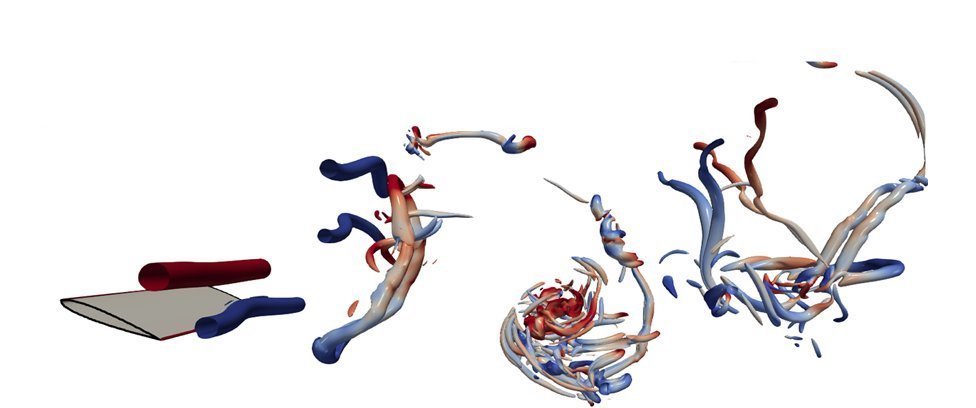
Large Eddy Simulation (LES) of turbulent flows relies on subgrid-scale models as well as wall models. The latter are crucial to applications of LES to wall-bounded flows that do not use sufficiently fine resolution to capture the viscous sublayer physics of the flow. The classical equilibrium wall model for Large Eddy Simulations (LES) assumes, among others, that the wall shear stress has the same direction as the LES velocity at the wall model matching location. However, for flows exhibiting separation due to adverse pressure gradients this assumption is invalid when the matching location lies above the near-wall reversed flow region. The presentation will summarize recent work extending the Moody diagram-based wall modeling method to incorporate velocity profiles with near-wall reversed flow. To avoid solving an ordinary differential equation to find the local wall stress during LES, the equation is solved off-line. The solution is fitted with highly accurate fitting functions, including in a parameter regime for which unresolved reverse flow occurs (strong adverse pressure gradient and low-to-moderate local Reynolds number). Analytic solutions are used to smoothly connect various asymptotic limits. The extended Moody diagram-based wall model is applied in LES of turbulent flow over periodic hills that exhibits local flow separation. While the wall model effect on mean velocity profiles is less easily elucidated due to additional dependencies on subgrid-scale model details and how the stress boundary condition is imposed, LES with the proposed extended Moody wall model yields improved predictions of the wall stress in the region where a small separation bubble occurs below the matching height. In the second part of the presentation, the speaker will discuss modeling wall bounded turbulent flows over rough surfaces, and a new physics-based parameter, the wind-shade factor, to determine the roughness length from purely geometric (topographical) information about the surface.

Biography

Charles Meneveau is the Louis M. Sardella Professor in the Department of Mechanical Engineering, is Associate Director of the Institute for Data Intensive Engineering and Science (IDIES) and is jointly appointed as Professor in the Department of Physics and Astronomy at Johns Hopkins University. He received his B.S. degree in Mechanical Engineering from the Universidad Técnica Federico Santa María in Valparaíso, Chile, in 1985 and M.S, M.Phil. and Ph.D. degrees from Yale University in 1987, 1988 and 1989, respectively. During 1989-1990 he was a postdoctoral fellow at the Center for Turbulence Research at Stanford. He has been on the Johns Hopkins faculty since 1990. His area of research is focused on understanding and modeling hydrodynamic turbulence, and complexity in fluid mechanics in general. The insights that have emerged from Professor Meneveau’s work have led to new numerical models for Large Eddy Simulations (LES) and applications in engineering and environmental flows, including wind farms. He also focuses on developing methods to share the very large data sets that arise in computational fluid dynamics. He is Deputy Editor of the Journal of Fluid Mechanics and has served as the Editor-in-Chief of the Journal of Turbulence. Professor Meneveau is a member of the US National Academy of Engineering, a foreign corresponding member of the Chilean Academy of Sciences, a Fellow of APS, ASME, AMS and recipient of the 2024 Batchelor Prize in Fluid Mechanics, the 2021 Fluid Dynamics Award from the AIAA, the Stanley Corrsin Award from the APS, the JHU Alumni Association's Excellence in Teaching Award, and the APS' François N. Frenkiel Award for Fluid Mechanics.